
イーサリアムの採掘工程を抑えてガス代を節約
この記事は、コンピュータ-のマイニング時のふるまいから「ガス代の節約が可能ではないのか?」という仮説を元にしており、一般的な”時間やタイミングによってガス代を安く(節約)する”というものとは一線を画します。
実証試験結果も掲載しておりますので、是非ご覧ください。
実験結果から
まずは、下図をご覧ください。
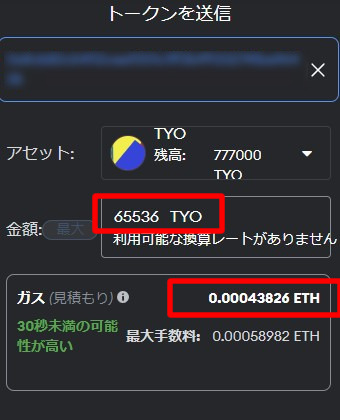
これは、MetaMaskから暗合資産の取引会社のWalletに、TYO(トークンを)送る直前のキャプチャーです。
65536TYOを送信する依頼をしていて、ガス代の見積もりは0.000432826ETHと提示されています。
次の画像は、送信した直後の結果です。
ガス代合計 0.000182ETHと表示されています。
送信前の提示額の半額以下です。
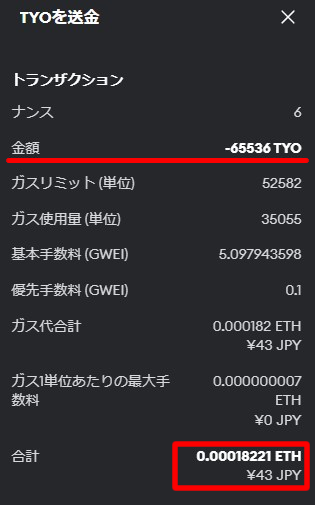
つまり、見積もられたガス代を安くしてトークンを送信することに成功したことを意味します。
「成功した」と表現しますが、これは偶然ではなく、ある理論の元で意図的に行った実験結果です。
以降は、その理論について書き記し、最期に数例の実験結果をご紹介します。
ノイマン式コンピューターとビット
最初にPC(Personal Computer)の中を覗いてみましょう。複雑な構造ですが、この記事のテーマに関係する部分を、できるだけ簡単に表現してみます。
ガス代を安くするために最低限必要な知識が出てきますので、サクッと流し読みした後で、必要なときに戻ってきて再確認してもOKです。
0(ゼロ)と1(イチ)の世界
ノイマン式コンピューター(普通のPCやスパコン)は、半導体で動いています。
高電圧を半導体に通過させようとすると突き抜けます:半導体=導体
低電圧を半導体に通過させようとすると止められます:半導体=不導体
それを数値化すると
通電した=1
通電しなかった=0
となります。
これを応用したものがノイマン式コンピューターです。
ノイマン式コンピューターの特徴として「基本的に足し算しかできない」です。引き算はマイナスを足して計算します。
つまり、コンピューターは、どんな複雑な関数でも中身は足し算しかしていないことになります。
ビット(bit)の正体
次に動作基準です。コンピューターは、 0000 0000 の8桁を基準に動作しているのですが、この桁の数をビット(bit)と呼びます。
この8桁の1ビットは1バイトという単位で使われます。
1byte=8bit となるわけです。
すなわち、
1byteの最小値= 0000 0000
1byteの最大値= 1111 1111
となります。
10進数に直してみましょう。
0000 0000 = 0
1111 1111 = 286331153
1111 1111 は不規則な数字が出てきました。これはコンピューターにとっては扱いにくく、負荷の高い数値となります。
では、8bitを基準としたコンピューターが良く使う数字で見てみましょう。
10進数
8
16
32
64
128
256
512
1024
2048
4096
8192
16384
32768
65536
これらの10進数は16進数で扱われる切りの良い数字となります。
では、2進数に直してみましょう。
2進数
8 1000
16 00010000
32 00100000
64 01000000
128 00100000
256 10000000
512 001000000000
1024 010000000000
2048 100000000000
4096 100000000000
8192 0001000000000000
16384 0100000000000000
32768 1000000000000000
65536 00010000000000000000
気が付きましたでしょうか。
どれも1が1つしか出てきません。
256bitとマイニングの関係についての仮説
ガス代と2進数の関係を紐解く
ここで、ブロックチェーンを考えてみましょう。
ブロックチェーンに使われるSHA256は256桁の2進数です。マイニングは、最も小さな値から順に総当たりする方法で正解を探します(逆に上から探す場合もある)。
このことから考えると、1桁に要する工数は以下のようになります。
正解が0の場合=1工数
正解が1の場合=2工数
0と1では2倍の工数差があることがわかります。
以下の工数を比べてみると
0000 0000 0000 0000 = 16工数
0001 0000 0000 0000 = 17工数
1111 1111 1111 1111 = 32工数
となります。
この工数がマイニングに要する総当たりの回数となり、それがマイニング時間とマイニングの費用となります。つまり、
ポイント
マイニング工数を減らすことでガス代を節約出来る
というのがここでの仮説です。
【実践】マイニングの工数計算
では、具体的な数字を使って工数を計算してみましょう。そして、マイニングの工数を減らす検討を行います。
1,000,000(100万)送金するとします。
最初に2進数に変換します。
11110100001001000000
となり、1が7つ、27工数になります。
ここで、100万に近い数字で工数を減らせる数字を探し当てます。ある種のマイニングですね。
前出の「ノイマン式コンピューターとビット」で記述した法則で探してみましょう。
答えから言うと、1,048,576です。
この数字を2進数に変換して確認しましょう。
000100000000000000000000
です。
1は1つ、25工数です。2工数減りました。
送金数量は増えるのに1の数を減らしたので、マイニングの工数を減らすことが出来ました。
”1”を減らすための豆知識
”1”が少なくなる例としては、以下の2つを覚えておくと良いでしょう。
ポイント2つ
- 8の倍数
- 256の倍数
です。
【簡単】2進数への変換方法
10進数から2進数への変換は、Windowsの電卓が便利です。
Windowsの電卓には10進数・16進数・2進数の変換ができる機能”プログラマーモード”があります。
DEC(10進数)を選択して数値を打ち込むと、BIN値のところに2進数が表示されます。
ここで1の数を数えることが出来ます。
以上が、ガス代と2進数の関係についての仮説です。
これに基づいて、実際にトークンを利用して実証実験を行いました。
ガス代の実証試験結果
これまでの理屈と仮説が本当に正しいのかどうか、実際にガス代を安くできるかどうかの実証実験を行いました。

TYOトークンを送金
下記の条件で送金実験を行いました。
実験概要
日時:2023年10月9日 17時頃(日本時間)
使用暗号資産:TYOトークン(ERC-20)
送信元:MetaMask
送信先:BitForexのTYOウォレット
【送金数量】
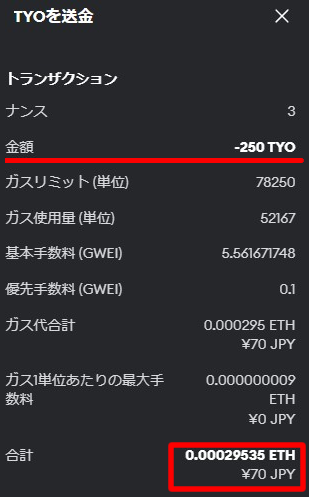
①250 TYO(256未満)
2進数:11111010(14工数)
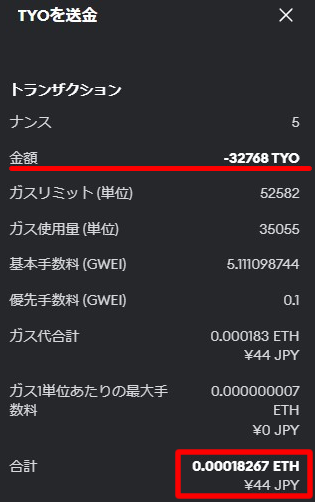
②32768 TYO(8x8x8x8x8)
2進数:1000000000000000(17工数)
③65536 TYOを送金(256x256)
2進数:00010000000000000000(21工数)
ガス代は安くなるのか?
上記の要領で送金を行った結果、下表のようになりました。
| 送金数量 | ガス代 |
| 250 TYO(256未満) | ¥70 |
| 32768 TYO | ¥44 |
| 65536 TYO | ¥43 |
この結果から言えることは、8の倍数で送るとガス代は安くなる。送金数量が多くても、マイニングにかかる工数が少ないとガス代が安くなる。ガス代の最小値は40円くらい(推定)。といったところでしょうか。
いずれにしても、最初に立てた仮説通りの結果となりました。
この試験での考察
実験としては、サンプルが少なすぎましたが、私自身は、イーサリアム(ERC-20)の送金時には、今後もこのような考えで送金数量を割り当てる予定です。サンプルが増えたら掲載します。
なお、どのくらいの工数を減らすと、どのくらいのガス代が節約出来るのかというところまでは踏み込んでいません。もしかすると、工数は減ったけど期待したほどガス代を節約出来なかった、という結果になるかもしれません。
また、送金時間ですが、65536TYOを送金した際のナンス6では10秒くらいで完了したのに対して、250TYOの送金時のナンス3で要した時間は1分くらいでした。
送金時間を記録することを失念しましたが、ガス代の節約はマイニングの工数を減らすこと=マイニング時間を短縮化という仮説が、ここでも当てはまると言うことが確認できたと思います。
以上。
【付録】図解~Windowsの電卓の使い方
Windowsの「スタートボタン」をクリックすると、アプリの一覧に「電卓」が表示されますので、クリックして起動させます。
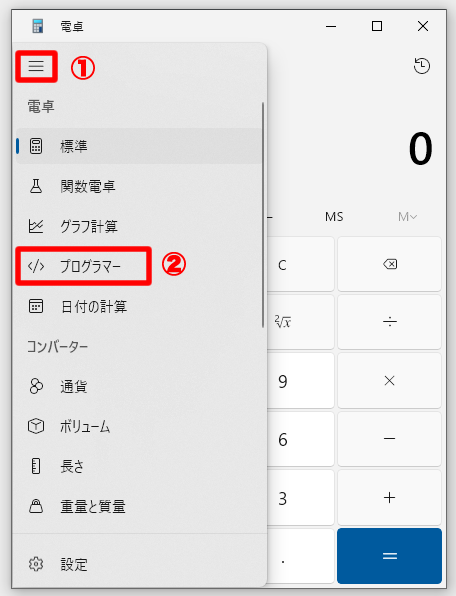
Windows電卓が起動したらメニュー(三)をクリックして、「プログラマー」を選択します。
プログラマーモードになりました。
デフォルトで10進数モード【DEC】になっていますので、そのまま数字を入力して下さい。
「BIN」のところに表示される数字が2進数です。
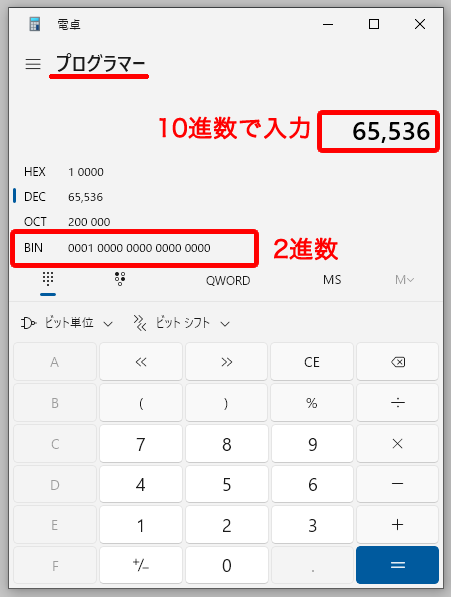
メモ
HEX:16進法
DEC:10進法
OCT:8進法
BIN:2進法
-

-
関連記事ビットコインの採掘(マイニング)とは
ブロックチェーンの正当性をチェック ナンス探しの競争原理 計算方法も答えも公開されている状態でのナンス探しですが、この正解を得るための特定の方程式などはありません。そこで、適当な文字列をナンスに入れて ...
続きを見る